[Algorithm] 백준 14891 - 구현 / 톱니바퀴
백준 실버 ~ 골드 문제를 풀며 정리한 내용입니다.
https://www.acmicpc.net/problem/14891
문제
총 8개의 톱니를 가지고 있는 톱니바퀴 4개가 아래 그림과 같이 일렬로 놓여져 있다. 또, 톱니는 N극 또는 S극 중 하나를 나타내고 있다. 톱니바퀴에는 번호가 매겨져 있는데, 가장 왼쪽 톱니바퀴가 1번, 그 오른쪽은 2번, 그 오른쪽은 3번, 가장 오른쪽 톱니바퀴는 4번이다.

이때, 톱니바퀴를 총 K번 회전시키려고 한다. 톱니바퀴의 회전은 한 칸을 기준으로 한다. 회전은 시계 방향과 반시계 방향이 있고, 아래 그림과 같이 회전한다.
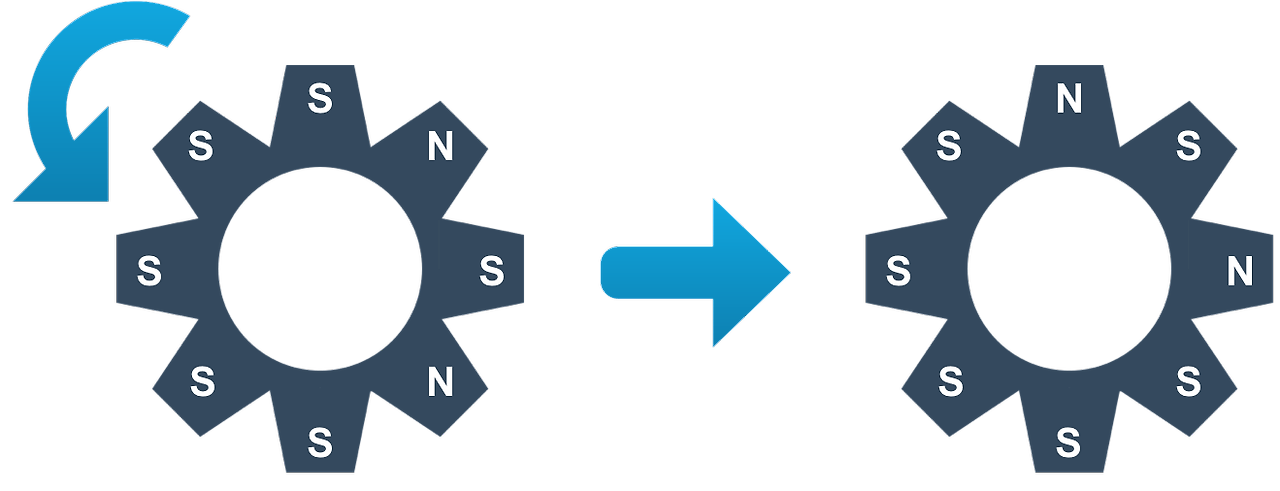

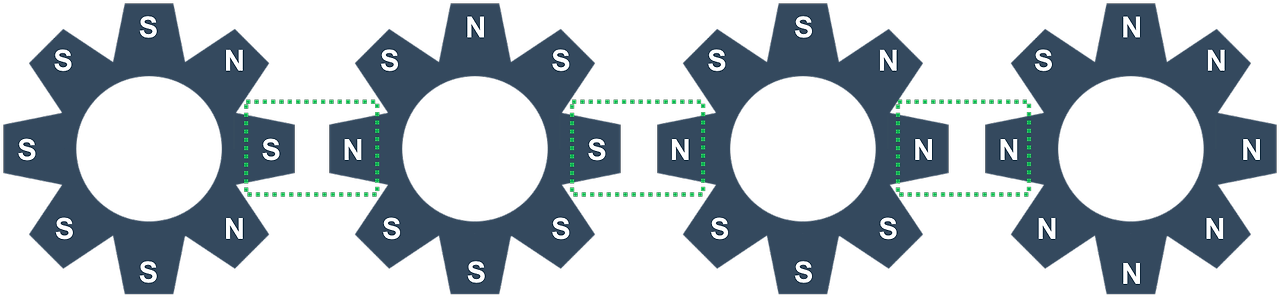
톱니바퀴를 회전시키려면, 회전시킬 톱니바퀴와 회전시킬 방향을 결정해야 한다. 톱니바퀴가 회전할 때, 서로 맞닿은 극에 따라서 옆에 있는 톱니바퀴를 회전시킬 수도 있고, 회전시키지 않을 수도 있다. 톱니바퀴 A를 회전할 때, 그 옆에 있는 톱니바퀴 B와 서로 맞닿은 톱니의 극이 다르다면, B는 A가 회전한 방향과 반대방향으로 회전하게 된다. 예를 들어, 아래와 같은 경우를 살펴보자.

두 톱니바퀴의 맞닿은 부분은 초록색 점선으로 묶여있는 부분이다. 여기서, 3번 톱니바퀴를 반시계 방향으로 회전했다면, 4번 톱니바퀴는 시계 방향으로 회전하게 된다. 2번 톱니바퀴는 맞닿은 부분이 S극으로 서로 같기 때문에, 회전하지 않게 되고, 1번 톱니바퀴는 2번이 회전하지 않았기 때문에, 회전하지 않게 된다. 따라서, 아래 그림과 같은 모양을 만들게 된다.
위와 같은 상태에서 1번 톱니바퀴를 시계 방향으로 회전시키면, 2번 톱니바퀴가 반시계 방향으로 회전하게 되고, 2번이 회전하기 때문에, 3번도 동시에 시계 방향으로 회전하게 된다. 4번은 3번이 회전하지만, 맞닿은 극이 같기 때문에 회전하지 않는다. 따라서, 아래와 같은 상태가 된다.

톱니바퀴의 초기 상태와 톱니바퀴를 회전시킨 방법이 주어졌을 때, 최종 톱니바퀴의 상태를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 1번 톱니바퀴의 상태, 둘째 줄에 2번 톱니바퀴의 상태, 셋째 줄에 3번 톱니바퀴의 상태, 넷째 줄에 4번 톱니바퀴의 상태가 주어진다. 상태는 8개의 정수로 이루어져 있고, 12시방향부터 시계방향 순서대로 주어진다. N극은 0, S극은 1로 나타나있다.
다섯째 줄에는 회전 횟수 K(1 ≤ K ≤ 100)가 주어진다. 다음 K개 줄에는 회전시킨 방법이 순서대로 주어진다. 각 방법은 두 개의 정수로 이루어져 있고, 첫 번째 정수는 회전시킨 톱니바퀴의 번호, 두 번째 정수는 방향이다. 방향이 1인 경우는 시계 방향이고, -1인 경우는 반시계 방향이다.
출력
총 K번 회전시킨 이후에 네 톱니바퀴의 점수의 합을 출력한다. 점수란 다음과 같이 계산한다.
- 1번 톱니바퀴의 12시방향이 N극이면 0점, S극이면 1점
- 2번 톱니바퀴의 12시방향이 N극이면 0점, S극이면 2점
- 3번 톱니바퀴의 12시방향이 N극이면 0점, S극이면 4점
- 4번 톱니바퀴의 12시방향이 N극이면 0점, S극이면 8점
- 예제 입력
10101111
01111101
11001110
00000010
2
3 -1
1 1
- 예제 출력
7
📌 풀이
2차원 배열을 선언해 각 톱니바퀴의 번호와 N/S극 상태 정보를 저장해 이용한다. K번의 회전을 반복하며 몇번 톱니바퀴를 어느 방향으로 돌릴지 확인하고 그 기준이 되는 톱니바퀴의 양쪽 톱니바퀴를 회전시킬지 안시킬지를 판단한다.
기준 톱니바퀴와 왼쪽 톱니바퀴는 기준 톱니바퀴의 6번 인덱스의 극(N -> 0, S -> 1)과 왼쪽 톱니바퀴의 2번 인덱스의 극을 비교해 두 극이 다른 경우 왼쪽 톱니바퀴를 회전시킨다. 기준 톱니바퀴와 오른쪽 톱니바퀴는 기준의 2번 인덱스 극과 오른쪽의 6번 인덱스를 기준으로 극을 비교해 다른 경우 오른쪽 톱니바퀴를 회전시킨다.
이때 판단(leftJudge / rightJudge)에 의해 양쪽 극이 같아 회전을 안하게 되면 그 이후의 왼쪽 오른쪽 톱니바퀴는 당연히 회전하지 못하므로 그대로 return해 함수 진행을 끝낸다. 회전을 하게 된다면 그 이후의 왼쪽 오른쪽 톱니바퀴의 회전 여부를 또 판단해야 한다. 각 판단 함수 안에 조건을 만족하지 않을(각 극이 다른) 경우 해당 함수를 또 호출하도록 재귀를 사용해 반복해서 판단한다. 이때 톱니바퀴는 1 ~ 4번까지만 존재하기 때문에 왼쪽을 기준으로 1번(0번 인덱스) 보다 작으면, 오른쪽을 기준으로 4번(3번 인덱스)보다 크면 그대로 함수 진행을 종료한다.
톱니바퀴를 회전시키기 이전에 각각 왼쪽 오른쪽 톱니바퀴가 돌아갈지 안돌아갈지를 먼저 판단하고 톱니바퀴를 회전시켜야 한다. 돌리는 함수가 먼저 호출되고 판단을 이후에 하게되면 판단 결과가 당연하게도 달라지기 때문이다. 함수 순서를 정확히 지켜 (판단 -> 회전) 순으로
호출한다. 판단 이후에 회전 함수를 호출해 각 톱니바퀴 번호와 방향에 맞게 회전시켜준다.
톱니바퀴 상태 판단과 회전을 완료했다면, 문제에서 원하는 출력값을 구해야 한다. 여기서는 각 톱니바퀴의 12시 방향의 극에 따른 점수의 합산을 구해야 한다. 이때 12시 방향은 톱니바퀴 배열에서 각 톱니바퀴 번호의 0번째 인덱스 값을 의미하며, N극은 0으로 S극은 1로 저장해두었기 때문에 바로 점수에 이용할 수 있다. N극인 경우 0점일수밖에 없기 때문에 S극만 계산해준다. S극 점수 계산의 흐름을 보면 점수가 2의 제곱으로 진행되기 때문에 그에 맞춰서 Math.pow를 통해 계산하고 출력해주었다.
톱니바퀴의 회전과 판단의 인덱스가 이해되지 않는다면 그림을 그려보자! 바로 이해가 된다 :)
구현
import java.util.*;
import java.io.*;
public class Main {
public static StringTokenizer st;
public static int[][] wheel = new int[4][8];
public static void main (String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
for (int i = 0; i < 4; i++) {
String s = br.readLine();
for (int j = 0; j < 8; j++) {
wheel[i][j] = s.charAt(j) - '0';
}
}
int K = Integer.parseInt(br.readLine());
for (int i = 0; i < K; i++) {
st = new StringTokenizer(br.readLine());
int wheelNum = Integer.parseInt(st.nextToken()) - 1;
int dir = Integer.parseInt(st.nextToken());
judgeWheel(wheelNum, dir);
}
int result = 0;
for (int i = 0; i < 4; i++) {
result += Math.pow(2, i) * wheel[i][0];
}
System.out.println(result);
}
public static void judgeWheel (int num, int dir) {
leftJudge(num - 1, -dir);
rightJudge(num + 1, -dir);
rollWheel(num, dir);
}
public static void leftJudge(int num, int dir) {
if (num < 0) return;
if (wheel[num][2] == wheel[num + 1][6]) return;
leftJudge(num - 1, -dir);
rollWheel(num, dir);
}
public static void rightJudge(int num, int dir) {
if (num > 3) return;
if (wheel[num][6] == wheel[num - 1][2]) return;
rightJudge(num + 1, -dir);
rollWheel(num, dir);
}
public static void rollWheel(int num, int dir) {
if (dir == 1) {
int tempR = wheel[num][7];
for (int i = 7; i > 0; i--) {
wheel[num][i] = wheel[num][i - 1];
}
wheel[num][0] = tempR;
} else {
int tempL = wheel[num][0];
for (int i = 0; i < 7; i++) {
wheel[num][i] = wheel[num][i + 1];
}
wheel[num][7] = tempL;
}
}
}